Covariance matrix adaptation

Hi, this post was written nearly a year ago in 2024, but my website wasn't functional until 2025. Previously there was a research experiment applying covariance matrix adaptation to a type of machine learning problem called "reinforcement learning", but this experiment never finished due to the lack of computational resources. This post is basically just a dump of what I learned about covariance matrix adaptation

In mathematics, there is a concept known as optimization, which means to find the optimal parameters that minimize or maximize an dependent value. In machine learning, we have models that can be represented as a box that takes an input and produces an output. The models have parameters, and adjusting the parameters adjusts the output of the model. There is a function known as the "loss function" that returns a measure of the error of our model for a given input. The goal of machine learning is to minimize the value outputted by our loss function to make our model more accurate. Typically in the industry this is done through some form of "gradient descent" algorithm

Gradient Descent

The most basic gradient descent algorithm, the stochastic gradient descent algorithm is defined as

$w_{t+1} = w_t - \alpha \nabla f(w_t)$

where $w_t$ is the value of a given parameter at step $t$ and $f(w_t)$ is the loss function for a given set of parameters

the $\nabla$ symbol (pronounced as "nabla") means take the "gradient" of the loss. The gradient represents the "rate of change" of the loss for the change in a parameter.

So what does this all mean? what we can see is that the algorithm takes the current parameter of the model, and subtracts a multiple $\alpha$ of the gradient from it.

Since the gradient represents the rate of change, of the loss, with respect to the current parameter values, a positive gradient means increasing the weight increases the loss, and a negative gradient means decreasing the weight decreases the loss this means by "moving" the parameters against the direction of the gradient, the loss should decrease.

However, there is one problem, and that is that the gradient is only calculated at the parameter value itself, meaning that sometimes gradients can be misleading and lead to only calculating the "local minima" of the loss function, and missing out on potential rewards, for example

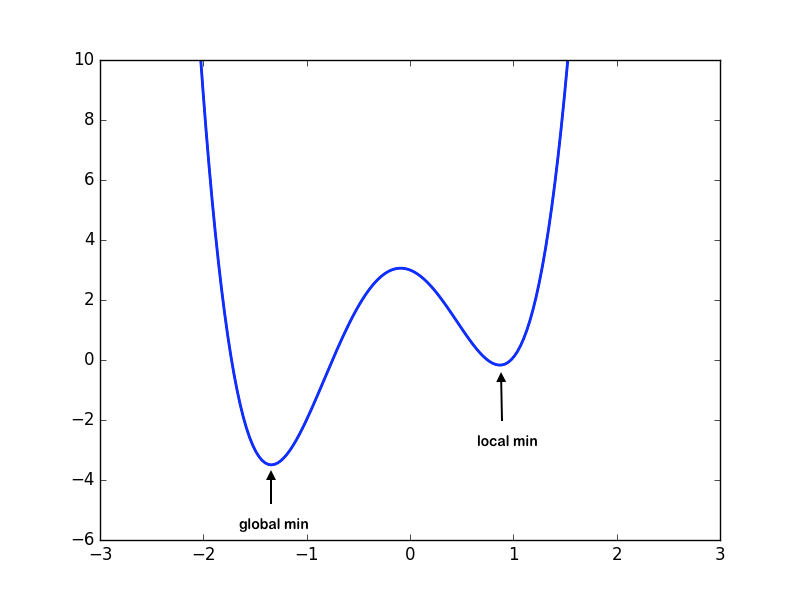Source: University of Illinois CS 357

here the gradient calculations close to local min would result in the algorithm converging on the local minima for small values of $\alpha$, and the algorithm would never be able to converge on the better solution at the global min

Evolution Strategies

Evolution strategies is an alternative less used method of optimization. It doesn't rely on gradients. The most basic form of evolution strategies "gaussian evolution strategies" work by generating a "population" of different configurations of parameters. From that population, the best performing (lowest loss) members are chosen and a new population is generated by using the statistical distribution of the best performing members, and the cycle is repeated.

However, there is one major issue of guassian evolutionary strategies. Since the best performing members is a subset of the entire population, the best performing members must have a lower standard deviation than the entire population, meaning over time the populations standard deviation increase, and the speed of the optimization decreases over time, making this a very slow optimization method.

This is where our hero "covariance matrix adaptation" comes in to fix this problem. Covariance matrix adaptation stores the direction that the mean of the population moves. If consecutive steps are in the same direction, the standard deviation (known as step size in covariance matrix adaptation) is increased to allow the algorithm to move faster as search larger areas. If consecutive steps are in different directions, the step size is decreased to allow the algorithm to converge quickly on a solution.

Gaussian Evolution Strategies	Covariance Matrix Adaptation

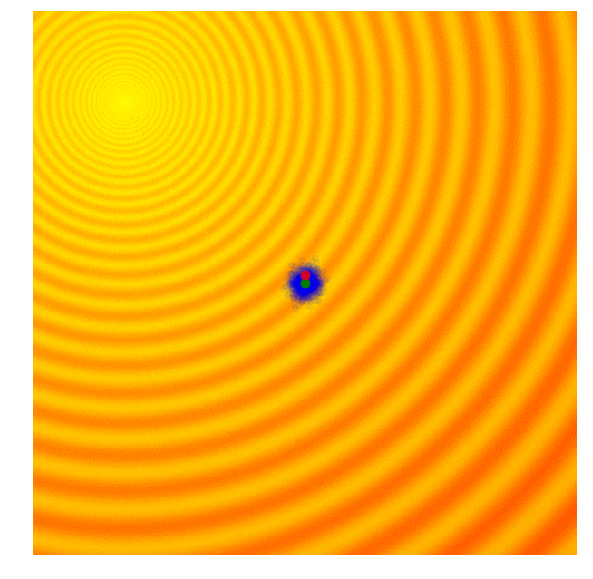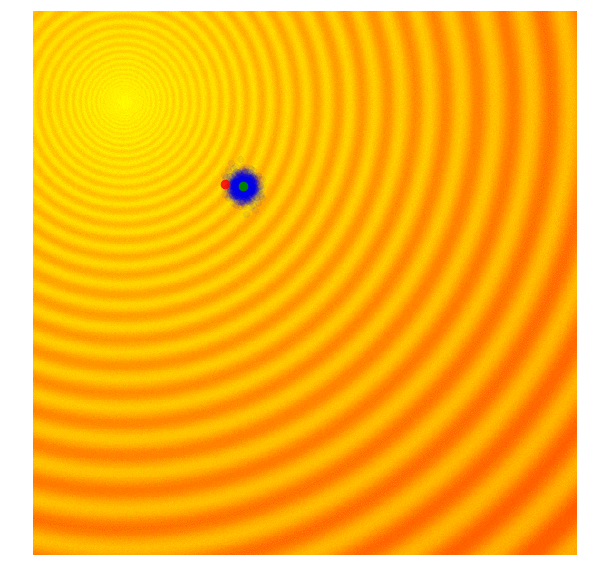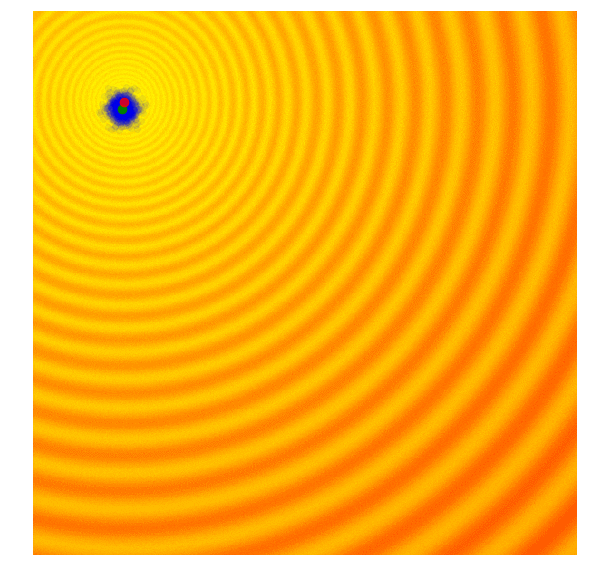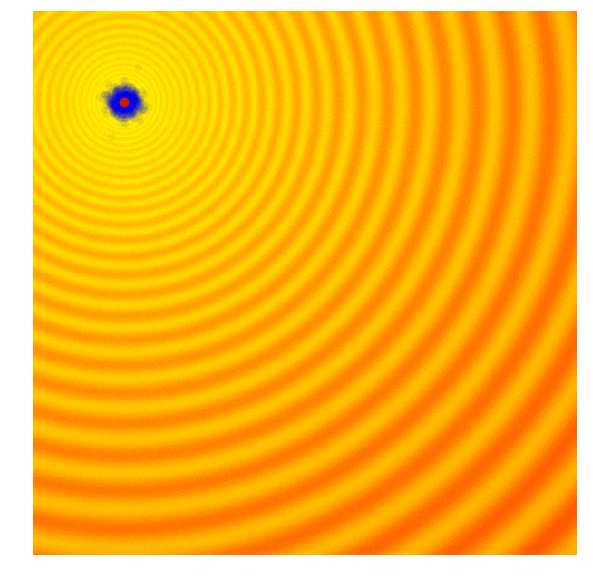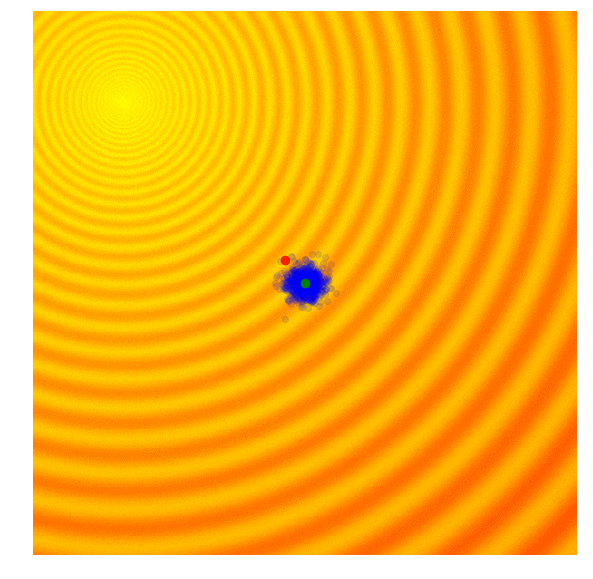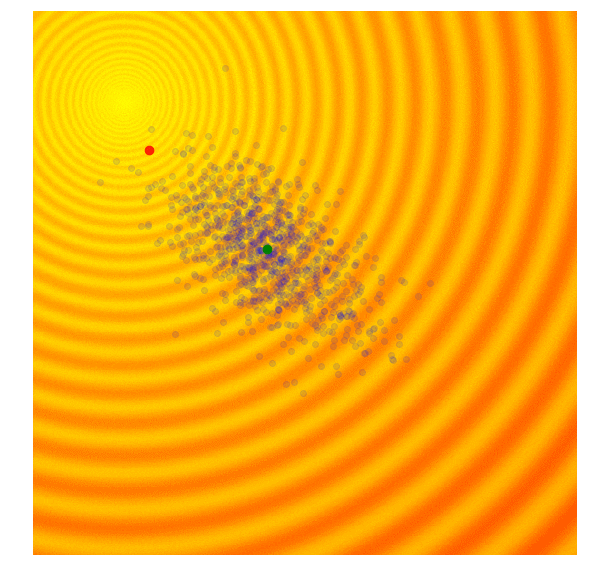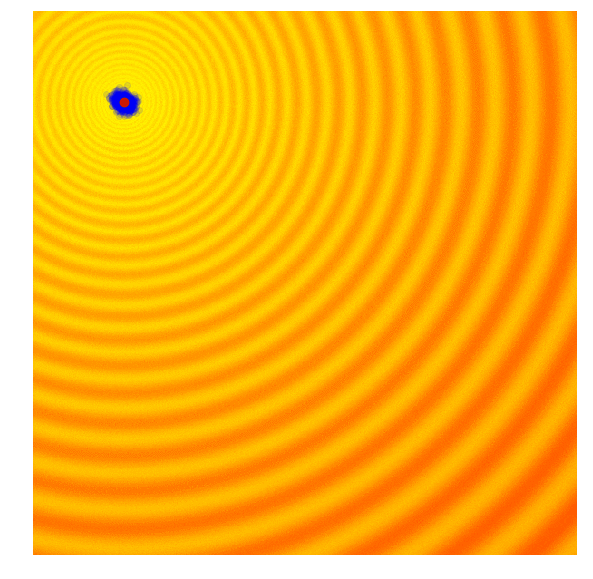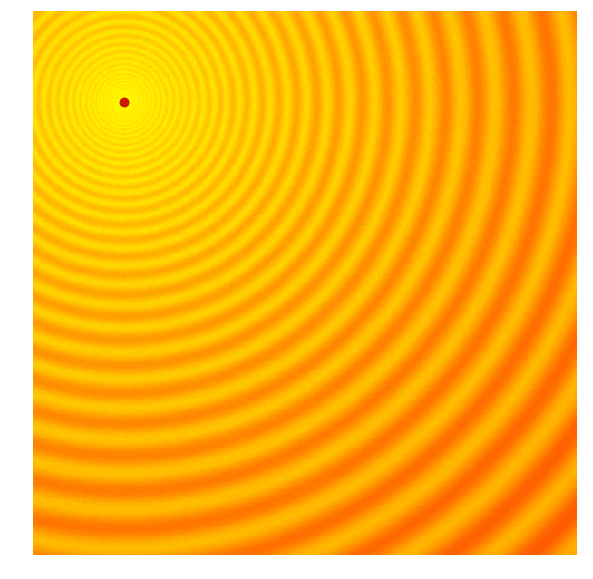Source: blog.otoro.net

My covariance matrix adaptation implementation

My implementation of covariance matrix adaptation can be found on my github repository for my machine learning in rust project called Milkshake, the same repo contains a few unfinished reinforcement learning experiments using covariance matrix adaptation.